practicas

FORMATO CONDICIONAL EN EXCEL

El formato condicional en Excel es una funcionalidad de gran utilidad al momento de realizar el análisis de datos ya que puedes dar un formato especial a un grupo de celdas en base al valor de otra celda. Esto te permitirá aplicar un tipo de fuente específico o un color de relleno diferente para aquellas celdas que cumplan con ciertas reglas y así poder identificarlas fácilmente en pantalla. Esta es una serie de artículos que te ayudará a comprender mejor este concepto.

El formato condicional en Excel es una manera de hacer que la herramienta aplique un formato especial para aquellas celdas que cumplen con ciertas condiciones. Por ejemplo, se puede utilizar el formato condicional para cambiar el color de las celdas que tienen un valor negativo.

Razón para utilizar el formato condicional

Siempre tienes la opción de aplicar manualmente un formato a cada una de las celdas que cumplen con una condición, pero eso se puede convertir en un proceso largo y repetitivo, especialmente si tienes una tabla de datos muy grande y que cambia frecuentemente. Es por eso que el formato condicional puede hacer más fácil la tarea de cambiar automáticamente el formato de la celda que cumple con ciertos criterios.

Ejemplos de formato condicional

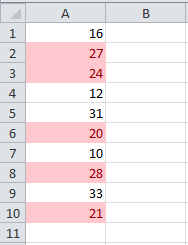
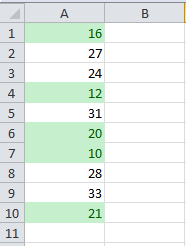
Formato especial para todos los valores entre 20 y 30:

Resaltar los valores por debajo del promedio (Para este ejemplo el promedio es 22.2).

¿Cómo se aplica el formato condicional?

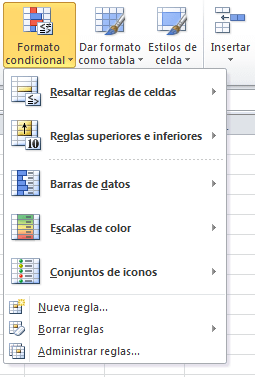
Debes selccionar las celdas a las que se les aplicará el formato condicional y después hacer clic en el comandoFormato condicional que aparece en el grupo Estilos de la ficha Inicio.

Como ya mencioné previamente, al seleccionar alguna de las opciones del menú, el formato se aplicará para aquellas celdas que cumplan con cierta condición o regla. Un formato condicional en Excel está siempre basado en una regla que posteriormentre se podrá editar si así lo deseas. Las reglas que se crean para los formatos condicionales se pueden dividir en dos grandes grupos:

• Reglas basadas en valores de celda: Estas reglas se basan en el mismo valor de la celda (Mayor que, Menor que, Igual a, Entre, etc.).
• Reglas basadas en fórmulas: Estas reglas ofrecen mayor flexibilidad porque puedes aplicar un formato especial utilzando una fórmula donde podrás aplicar una lógica más compleja. Por lo mismo es un poco más complicado de aprender, pero una vez que lo hagas seré muy intuitivo de utilizar

Productos notables y factorizacion

ACTIVIDAD 4

DÍA DE MUERTOS

DÍA DE MUERTOS

VÍDEO DE ESTUDIANTES NO MEXICANOS

En este vídeo nos muestra que la niña va a visitar al panteón a su mama, como se acostumbra en México visitar a tus familiares cada dia de muertos, Luego se encuentra una flor y"baja al mundo de los muertos" donde se encuentra con un festividad muy bonita, como lo haríamos en la tierra. Y luego se da cuenta que solo era un sueño pero en realidad su mama quería pasársela muy bien con ella. 

VÍDEO DE ESTUDIANTES MEXICANOS

El vídeo me conmovió mucho ya que la verdad aveces no recordamos a nuestros seres que ya pasaron a otra etapa de la vida que es la naturaleza de los humanos: nacer, crecer , reproducirse , morir así  es la ley humana. También aveces por el trabajo o la vida ordinaria olvidamos celebrar estas fechas, También el vídeo habla que todos los seres humanos vamos a donde mismo, así sean famosos o no todos en algún momento pasaremos por lo mismo.Y el señor que se muestra en el vídeo se encuentra muy feliz, Así que en México que algunos estados el "DÍA DE MUERTOS" es una fecha alegre y la gente festeja porque el difunto esta bien, se dice que no piensan que es una fecha triste si no de alegría porque ya no están sufriendo. Es una costumbre muy peculiar aquí en México.

VÍDEO HECHO POR PROFESIONALES 

En este vídeo realmente no aparece nada sobre el día de muertos, si es de profesionales se supone que debían saber sobre el tema pero es sobre mi punto de vista. Lo que si esta muy bien hecho es el vídeo me pareció interesante la manera en que trabajaron con la computadora y la catrina que sale cantando es muy buena esa canción me pareció que era lo único que se acercaba con la realidad con el dia de muertos

En conclusión  a mi el día de muertos no me agrada tanto, para mi si es una fecha muy triste, solo me gusta por la festividad y por los altar de muertos muy bien elaborados. 

ÁLGEBRA ÁRABE

LENGUAJE DEL ALGEBRA ARABE

"Los árabes adquirieron el conocimiento de la ciencia griega a partir de dos fuentes. La mayor parte de ella la aprendieron de los griegos del Imperio bizantino, pero también la adquirieron, de segunda mano, de los cristianos nestorianos de habla siríaca de Persia oriental. Los cristianos nestorianos, desde su centro de Jundishapur, tradujeron durante los siglos VI y VII un importante número de obras griegas científicas -sobre todo de lógica y de medicina- al siríaco, que había reemplazado al griego como lengua culta del Asia occidental desde el siglo III. Después de la conquista árabe, Jundishapur continuó siendo durante un tiempo el primer centro científico y médico del Islam, donde cristianos, judíos y otros súbditos de los califas trabajaban en la traducción de textos del siríaco al árabe.

Los árabes introdujeron y mejoraron los símbolos del sistema numérico hindú y la notación posicional. También usaron los irracionales de la misma forma que lo hicieron los hindúes. Esto debe enfatizarse: Omar Khayyam (1048 - 1122) y Nasir-Eddin (1201 - 1274) afirmaron con toda claridad que las razones de magnitudes, conmensurables o inconmensurables, podían ser llamadas números. Resulta interesante, sin embargo, que aunque ellos conocían el uso de los números negativos y sus reglas de operación, introducidas por los hindúes, aún así los rechazaron. Con esto ya tenemos un primer retrato de la cultura islámica. Vamos ahora a entrar en mayor detalle en las matemáticas.

Se mencionan dos tradiciones en la astronomía y las matemáticas en Bagdad. Una con base en las fuentes persas e indias, que subrayaba una aproximación algebraica en las matemáticas, y también presente en las tablas astronómicas, y con una motivación práctica. En esa tradición se coloca al-Khwarizmi. Otra tradición con énfasis en las matemáticas helenísticas, que subrayaba la geometría y los métodos deductivos. Su figura emblemática: Tabit ibn Qurra. Ambas tradiciones se llegarían a fundir, lo que se podrá apreciar en el trabajo de Omar Khayyam y al-Kashi.

La contribución árabe a la trigonometría nos la reseña Bell de la siguiente forma:

"Los árabes adoptaron y desarrollaron la trigonometría hindú. El primer progreso notable se debió al astrónomo Al-Battani (muerto en el 929), en el siglo IX. Si bien en realidad no fue el primero que aplicó el álgebra en lugar de la sola geometría a la trigonometría, este astrónomo matemático fue el primero que dio un gran paso en esa dirección. Usó además del seno hindú, la tangente y la cotangente. En el siglo X se calcularon tablas de estas dos últimas, y también hicieron su aparición la secante y la cosecante como razones trigonométricas. Por estar el concepto de función todavía unos 600 años en el futuro, nada en su obra se parece mucho a la trigonometría elemental de hoy día.

De hecho, la función seno fue traída de la matemática india se supone que a través de un texto de astronomía india Surya Siddhanta. También  sensa alpha $ y sindatta  fueron incorporadas de los hindúes. Las funciones tangentes y cotangente sí son de origen árabe.

La trigonometría es la rama de las matemáticas que los árabes cultivaron con mayor entusiasmo, debido a su aplicación en la astronomía.

La impronta más relevante y significativa del saber científico árabe está relacionada con las matemáticas. Nuestras actuales cifras “arábigas” llegaron a occidente gracias a la aportación islámica, aunque en sus orígenes remotos fueron hindúes. También es árabe el concepto de “cero” y el término “

Numerosas fórmulas geométricas y aritméticas son igualmente herencia árabe. Se utilizaron ampliamente para calcular superficies (trigonometría), distancias o volúmenes.

Los árabes aportaron muchos términos importantes para las matemáticas, ahora son entendibles

MEMORAMA ALGEBRAICO

MEMORAMA ALGEBRAICO

INTRODUCCIÓN

Como sabemos, para memorizar los términos algebraicos tendríamos que estudiar y estudiar varias veces. En este caso no sera así, sera de una manera diferente ya que lo haremos dinámico, es decir, jugaremos al memorama. Para aprender varios conceptos y nos resulte fácil. 

1.-Concepto de termino algebraico:
es una expresión algebraica. Consta de un símbolo o varios símbolos no separados por + o -.
Contiene solamente multiplicaciones, divisiones, potencias y raíces. No contiene sumas ni restas. Contiene constantes  y variables. 
2.-Concepto de signo:
El signo puede ser positivo(+) o negativo (-). Cuando un termino no tiene ningún signo escrito se considera positivo. 
3.-Concepto de coeficiente:
Son cantidades cuyo valor permanece constante a lo largo de la resolución del problema. Puede ser un numero una letra, en cuyo caso su valor no cambiara al resolver el problema. 
4.-Concepto de variable:
Son cantidades cuyo valor no es conocido. Vamos a tomar la notación usual: se utilizaran las ultimas letras del alfabeto como variables y las primeras como constantes. Tomando en cuenta que podemos utilizar cualquier letra del alfabeto. 
5.-Concepto de exponente:
Indica la potencia a la que esta elevada, una variable, constante o incógnita. En la notación moderna se colocan arriba a la derecha de la cantidad que sera afectada por él.
 6.-Concepto de monomio:
Un monomio es una expresión algebraica en la que las únicas operaciones que aparecen entre las variables son el producto y la potencia del exponente natural. 
7.-Concepto de binomio: 
es una expresión algebraica formada por dos términos. Cualquier expresión formada por la suma o la resta de dos términos.
8.-Concepto de Trinomio:
Expresión que consta de tres términos. Esta compuesta por constantes y variables, vinculadas entre si , a través de multiplicación, resta y suma. 
9.-Concepto de Polinomio:
Se forman a partir de la unión de dos o más variables y constantes, vinculadas a través de operaciones de multiplicación, resta o suma, reciben el nombre de polinomios
10.-Concepto de grado respecto a una variable: 
es el máximo exponente que posee el monomio sobre la variable; Por ejemplo en 2x3 + 4x2 + x + 7, el término de mayor grado es 2x3; este término tiene una potencia tres en la variable x, y por lo tanto se define como grado 3 o de tercer grado
11.-Ejemplo de polinomio con mas de tres términos:

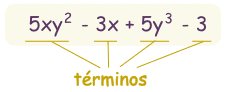
12.-Concepto de grado absoluto:
El grado absoluto de un monomio es la suma de los exponentes de todas y cada una de las letras.
13.-Literales utilizadas como constantes:
Utilizamos las primeras letras del abecedario como constantes (a,b,c)
14.-Concepto de expresión algebraica:
formada por números y por símbolos representados por letras (indicadores de incógnitas, pues indican cantidades que se deben averiguar) que se encuentran vinculados entre sí por medio de signos, que señalan las operaciones que se necesitan efectuar, ya sean sumas, restas, multiplicaciones, divisiones o potenciales.
15.- Ejemplo de términos semejantes:


16.-Ejemplo de termino con grado absoluto igual a 6:


17.-Ejemplo de binomio:


18.-Ejemplo de termino con grado 3 respecto a equis:

ax+ax²+ax³

19: ejemplo de termino con grado 3 respecto a y: 

5y³+8x+6x²

A CONTINUACIÓN, PARA PROBAR LOS CONOCIMIENTOS QUE ADQUIRÍ CON DICHA ACTIVIDAD. ESCRIBIRÉ LOS CONCEPTOS CON MI PROPIO CRITERIO.

1.-Concepto de termino algebraico: 
es todo termino que se representa con un símbolo, letra o numero.
2.-Concepto de signo:
son signos + o - para separar una expresión
3.-Concepto de coeficiente:
es un valor que permanece constante e indica cuantas veces se multiplicara.
4.-Concepto de variable:
son cantidades que no son exactas y se van a cambiar constantemente. 
5.-Concepto de exponente:
Indica la potencia a la que se elevara cualquier numero y se encuentra arriba a la derecha.
6.-Concepto de monomio:
son expresiones que constan de un termino, y las podemos utilizar en sumas, restas y multiplicaciones.
7.-Concepto de binomio:
son expresiones que constan de dos términos, al igual que el monomio con operaciones básicas. Pero estas separadas por el signo + o -.
8.-Concepto de trinomio:
son expresiones que constan de tres términos, igual con operaciones básicas.
9.-Concepto de polinomio:
Son todas aquellas expresiones que constan de dos o mas términos, en cualquier operación básica. 
10.-Concepto de grado respecto a una variable:
es el máximo exponente en una variable , ya que este puede tener grado 3.
11.-Ejemplo de polinomio con mas de tres términos:

12.-Concepto de grado absoluto:
es la suma de todos los exponentes, pasando ha ser un numero natural.
13.-Literales utilizadas como constantes:
utilizamos como constantes las letras del alfabeto (a,b,c)
14.-Concepto de expresión algebraica:
es toda aquel termino o expresión que podemos representar con letras, números, exponentes y variables.
15.- Ejemplo de términos semejantes:
por ejemplo tengo 5x+3y no podemos realizar la operación ya que no tiene la misma letra y por lo tanto no son semejantes. 
16.-Ejemplo de termino con grado absoluto igual a 6:

17.-Ejemplo de binomio:
(5x+6x)+(6x-8x)
18.-Ejemplo de termino con grado 3 respecto a equis:

ax+ax²+ax³

19: ejemplo de termino con grado 3 respecto a y: 

5y³+8x+6x<sup>2 

REPORTE:</sup>
Hicimos el memorama en una clase ya que lo hicimos sencillo y rápido, Los materiales los compramos entre todo y fue muy bueno ya que todos nos unimos y trabajamos en equipo, Hicimos los últimos detalles en una clase libre, los conceptos los investigamos en libros, Internet y complementamos con nuestro propio criterio. Luego en un clase comenzamos a jugar con el memorama y se cumplió  el objetivo que queríamos aprendimos los conceptos de dichos términos algebraicos.

CONCLUSIÓN: 

La conclusión de todo esto fue buena, todos trabajamos y aprendimos, Esta actividad me gusto mucho ya que fue algo fuera de lo usual, y es mucho mas practico que estar estudiando por horas. Y a los alumnos que se les dificulta esto, se les hará mas fácil y dinámico empezar a aprender. Opino que deberíamos de hacer mas actividades como estas para trabajar entre todos y aprender. Y cumplimos con dicho objetivo que era deseado para desarrollar y comprender mejor todos estos temas. 

FUENTES DE INFORMACION:

vitutor 

definicion.de

epamatematicas.blogspot.mx

http://www.slideshare.net/licmata/trmino-algebraico-53800729

ACTIVIDAD 2.

NÚMEROS COMPLEJOS

Los números complejos conforman un grupo de cifras resultantes de la suma entre un número real y uno de tipo imaginario. 

Los números complejos son la herramienta de trabajo del álgebra, análisis, así como de ramas de las matemáticas puras y aplicadas como variable compleja, ecuaciones diferenciales, facilitación de cálculo de integrales, en aerodinámica, hidrodinámica y electromagnetismo entre otras de gran importancia. Además los números complejos se utilizan por doquier en matemáticas, en muchos campos de la física  (notoriamente en la mecánica cuántica) y en ingeniería, especialmente en la electrónica y las telecomunicaciones, por su utilidad para representar las ondas electromagnéticas y la corriente eléctrica. 
Los números complejos forman un cuerpo,  el cuerpo complejo, denotado por C (o más apropiadamente por el carácter unico de ℂ ). Si identificamos el número real a con el complejo (a, 0), el cuerpo de los números reales R aparece como un subcuerpo de C. Más aún, C forma un espacio vectorial  de dimensión 2 sobre los reales. Los complejos no pueden ser ordenados como, por ejemplo, los números reales , por lo que C no puede ser convertido de ninguna manera en un cuerpo ordenado. 

NÚMEROS IMAGINARIOS

Los números imaginarios son un tipo de numero  complejo cuyo origen gira en torno a la raíz cuadrada de menos 1. Para comprender mejor el concepto hay que repasar qué son las raíces cuadradas:

En las matemáticas pre-imaginarias (los números reales), cualquier número elevado por sí mismo, a excepción del cero, da un resultado positivo. Esta operación se denomina: “elevar al cuadrado“. Por ejemplo elevar dos al cuadrado sería: 2 · 2 = 2² = 4.

. LA RAÍZ CUADRADA DE -1

Realicemos un ejercicio de memoria lógica relacionado con el razonamiento anterior: si la raíz cuadrada es la operación inversa a elevar al cuadrado cualquier número, y el resultado de estos últimos son solo números positivos, las raíces cuadradas solo pueden realizarse en números positivos. Al menos, en las operaciones reales.

¿Qué ocurre cuando nos encontramos con una ecuación como la siguiente x² = -1?

Siguiendo las reglas tradicionales de las matemáticas, no se puede resolver, ya que x sería igual a √-1, una operación que antes hemos visto que no puede existir. Ante esta situación, los matemáticos propusieron una solución, sustituir ese valor por un número: el número i.

NÚMEROS REALES

Los números reales son los que pueden ser expresados por un número entero (3, 28, 1568) o decimal (4,28; 289,6; 39985,4671). Esto quiere decir que abarcan a los números racionales (que pueden representarse como el cociente de dos enteros con denominador distinto a cero) y los números irracionales (los que no pueden ser expresados como una fracción de números enteros con denominador diferente a cero).

Otra clasificación de los números reales puede realizarse entre números algebraicos (un tipo de número complejo) y números trascendentes (un tipo de número irracional).

Más concretamente nos encontramos con el hecho de que los números reales se clasifican en números racionales e irracionales. En el primer grupo se encuentran a su vez dos categorías: los enteros, que se dividen en tres grupos (naturales, 0, enteros negativos), y los fraccionarios, que se subdividen en fracción propia y en fracción impropia. Todo ello sin olvidar que dentro de los citados naturales también hay tres variedades: uno, naturales primos y naturales compuestos.

En el segundo gran grupo anteriormente citado, el de los números irracionales, nos encontramos a su vez que existen en su seno dos clasificaciones: irracionales algebraicos e intrascendentes.

Dentro de la Ingeniería se hace especialmente uso de los citados números reales y en ella se parte de una serie de ideas claramente delimitadas como serían las siguientes: los números reales son la suma de los racionales y los irracionales, el conjunto de los reales puede definirse como un conjunto ordenado y este se puede representar mediante una recta en la que cada punto de la misma representa a un número concreto.

Es importante tener en cuenta que los números reales permiten completar cualquier tipo de operación básica con dos excepciones: las raíces de orden par de los números negativos no son números reales (aquí aparece la noción de número complejo) y no existe la división entre cero (no es posible dividir algo entre nada).